Gadget3 suitability formulae

Formula-returning functions describing length suitability relationships.

g3_suitability_exponentiall50(
    alpha = g3_parameterized("alpha", by_stock = by_stock, by_predator = by_predator),
    l50 = g3_parameterized("l50", by_stock = by_stock, by_predator = by_predator),
    by_stock = TRUE,
    by_predator = TRUE)

g3_suitability_andersen(p0, p1, p2, p3 = p4, p4, p5 = quote( predator_length ))

g3_suitability_andersenfleet(
        p0 = g3_parameterized('andersen.p0', value = 0, optimise = FALSE,
                              by_stock = by_stock),
        p1 = g3_parameterized('andersen.p1', value = log(2),
                              by_stock = by_stock, by_predator = by_predator),
        p2 = g3_parameterized('andersen.p2', value = 1, optimise = FALSE,
                              by_stock = by_stock),
        p3 = g3_parameterized('andersen.p3', value = 0.1, exponentiate = exponentiate,
                              by_stock = by_stock, by_predator = by_predator),
        p4 = g3_parameterized('andersen.p4', value = 0.1, exponentiate = exponentiate,
                              by_stock = by_stock, by_predator = by_predator),
        p5 = quote( stock__maxmidlen ),
        by_stock = TRUE,
        by_predator = TRUE,
        exponentiate = TRUE)

g3_suitability_gamma(alpha, beta, gamma)

g3_suitability_exponential(alpha, beta, gamma, delta)

g3_suitability_straightline(alpha, beta)

g3_suitability_constant(
    suit = g3_parameterized("suit", by_stock = by_stock, by_predator = by_predator),
    by_stock = TRUE,
    by_predator = TRUE )

g3_suitability_richards(p0, p1, p2, p3, p4)

Arguments

suit,alpha,beta,gamma,delta,l50,p0,p1,p2,p3,p4,p5: formula substituted into calcuations, see below.
by_stock: Change the default parameterisation (e.g. to be by 'species'), passed through to default calls to g3_parameterized.
by_predator: Change the default parameterisation (e.g. to be by 'fleet'), passed through to default calls to g3_parameterized.
exponentiate: Exponentiate parameters,passed through to default calls to g3_parameterized.

Details

When using these to describe a predator/prey relationship, the stock midlength $l$ will refer to the prey midlength.

Value

All functions return a formula for use in g3a_predate_fleet's suitabilities argument:

g3_suitability_exponentiall50

A logarithmic dependence on the length of the prey as given by the following equation (note that the prey length dependence is actually dependant on the difference between the length of the prey and $l_{50}$):

$$ \frac{1}{ 1 + e^{-\alpha (l - l_{50})} } $$

$l$: Vector of stock midlength for each lengthgroup
$l_{50}$: Length of the stock with a 50% probability of predation, from parameter l50

g3_suitability_andersen

This is a more general suitability function that is dependant on the ratio of the predator length to the prey length as given by the following equation:

If $p_3 = p_4$: $$ p_0 + p_2 e^{-\frac{(x - p_1)^2}{p_4}} $$

Otherwise:

$$ p_0 + p_2 e^{-\frac{(x - p_1)^2}{p_4}} * \min(\max(p_1 - x, 0), 1) + p_2 e^{-\frac{(x - p_1)^2}{p_3}} * \min(\max(x, 0), 1) $$ ...i.e if $\log\frac{L}{l} <= p_1$ then $p_3$ used in place of $p_4$.

$x$: $\log\frac{p_5}{l}$
$L$: Vector of predator midlength for each lengthgroup
$l$: Vector of stock midlength for each lengthgroup
$p_0$ .. $p_4$: Function parameter p0 .. p4
$p_5$: Function parameter p5, if unspecified uses $L$, Vector of predator midlength for each lengthgroup.

NB: Specifying $p_5$ is equivalent to using the andersenfleet function in gadget2.

g3_suitability_andersenfleet

A simplified version of g3_suitability_andersen, suitable for predation by fleets, as the defaults do not rely on the predator's length.

g3_suitability_gamma

This is a suitability function that is more suitable for use when considering the predation by a fleet, where the parameter $\gamma$ would represent the size of the mesh used by the fleet (specified in centimetres).

$$ (\frac{l}{(\alpha - 1)\beta\gamma}) ^ {(\alpha - 1) e^{\alpha - 1 - \frac{l}{\beta\gamma}}} $$

$l$: Vector of stock midlength for each lengthgroup
$\alpha$: Function parameter alpha
$\beta$: Function parameter beta
$\gamma$: Function parameter gamma

g3_suitability_exponential

This is a suitability function that has a logarithmic dependence on both the length of the predator and the length of the prey as given by the following equation:

$$ \frac{\delta}{1 + e^{-\alpha - \beta l - \gamma L}} $$

$L$: Vector of predator midlength for each lengthgroup
$l$: Vector of stock midlength for each lengthgroup
$\alpha$: Function parameter alpha
$\beta$: Function parameter beta
$\gamma$: Function parameter gamma
$\delta$: Function parameter delta

g3_suitability_straightline

Returns a formula for use in predation function's suitabilities argument:

$$ \alpha + \beta l $$

$l$: Vector of stock midlength for each lengthgroup
$\alpha$: Function parameter alpha
$\beta$: Function parameter beta

g3_suitability_constant

Returns a formula for use in predation function's suitabilities argument:

$$ \alpha $$

$\alpha$: Function parameter suit, i.e. the "prey.predator.suit" model parameter by default

g3_suitability_richards

Returns a formula for use in predation function's suitabilities argument:

$$ {\big( \frac{p_3}{1 + e^{-p_0 - p_1 l - p_2 L}} \big)}^{\frac{1}{p_4}} $$

$L$: Vector of predator midlength for each lengthgroup
$l$: Vector of stock midlength for each lengthgroup
$p_0$ .. $p_4$: Function parameter p0 .. p4

This is an extension to g3_suitability_exponential.

Examples

ling_imm <- g3_stock(c(species = 'ling', 'imm'), seq(20, 156, 4)) %>% g3s_age(3, 10)
ling_mat <- g3_stock(c(species = 'ling', 'mat'), seq(20, 156, 4)) %>% g3s_age(5, 15)
igfs <- g3_fleet('igfs')

igfs_landings <-
  structure(expand.grid(year=1990:1994, step=2, area=1, total_weight=1),
            area_group = list(`1` = 1))

# Generate a fleet predation action using g3_suitability_exponentiall50
predate_action <- g3a_predate_fleet(
    igfs,
    list(ling_imm, ling_mat),
    suitabilities = list(
        ling_imm = g3_suitability_exponentiall50(
            g3_parameterized('lln.alpha', by_stock = 'species'),
            g3_parameterized('lln.l50', by_stock = 'species')),
        ling_mat = g3_suitability_exponentiall50(
            g3_parameterized('lln.alpha', by_stock = 'species'),
            g3_parameterized('lln.l50', by_stock = 'species'))),
    catchability = g3a_predate_catchability_totalfleet(
        g3_timeareadata('igfs_landings', igfs_landings)))

# You can use g3_eval to directly calculate values for a stock:
g3_eval(
    g3_suitability_exponentiall50(alpha = 0.2, l50 = 60),
    stock = g3_stock('x', seq(0, 100, 10)) )
#>         0:10        10:20        20:30        30:40        40:50        50:60 
#> 1.670142e-05 1.233946e-04 9.110512e-04 6.692851e-03 4.742587e-02 2.689414e-01 
#>        60:70        70:80        80:90       90:100      100:Inf 
#> 7.310586e-01 9.525741e-01 9.933071e-01 9.990889e-01 9.998766e-01 
#> attr(,"class")
#> [1] "force_vector" "numeric"     

## Plots
suit_plot <- function (
    suit_f,
    stock = g3_stock('x', seq(0, 100, 5)),
    predator_length = 140,
    cols = rainbow(5) ) {
  par(mar = c(2,2,2,2), cex.main = 1)

  for (a in seq_along(cols)) curve(
    g3_eval(
      suit_f,
      a = a,
      stock = stock,
      predator_length = predator_length )[x %/% g3_stock_def(stock, 'dl')[[1]] + 1],
    from = min(g3_stock_def(stock, 'minlen')),
    to = max(g3_stock_def(stock, 'minlen')),

    col = cols[[a]],
    main = deparse1(sys.call()[[2]]), xlab = "", ylab = "",
    add = (a != 1) )
}

suit_plot(g3_suitability_exponentiall50(alpha = ~a * 0.1, l50 = 50))

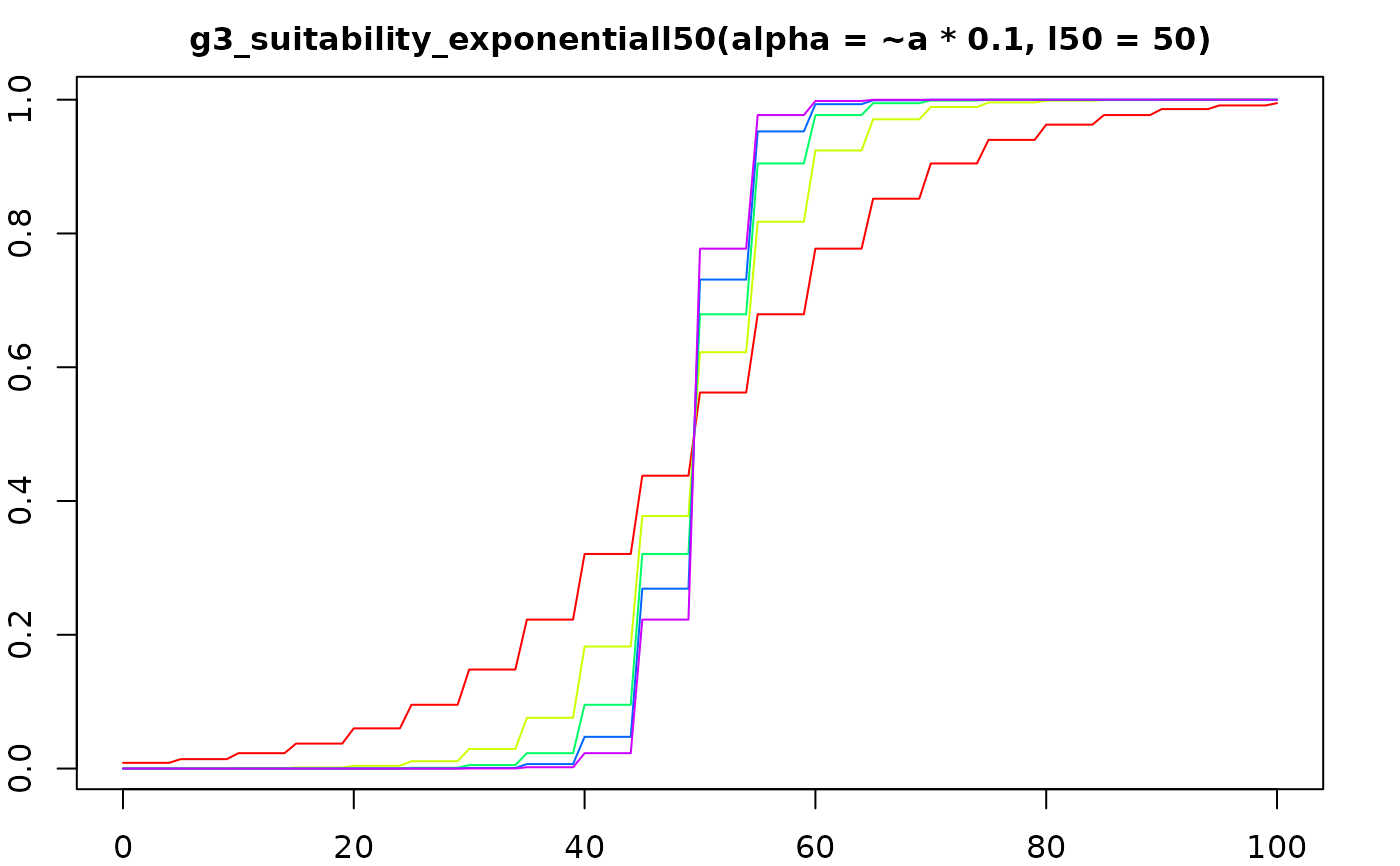suit_plot(g3_suitability_andersen(0, log(2), 1, p3 = ~a * 0.1, 0.1, 140))

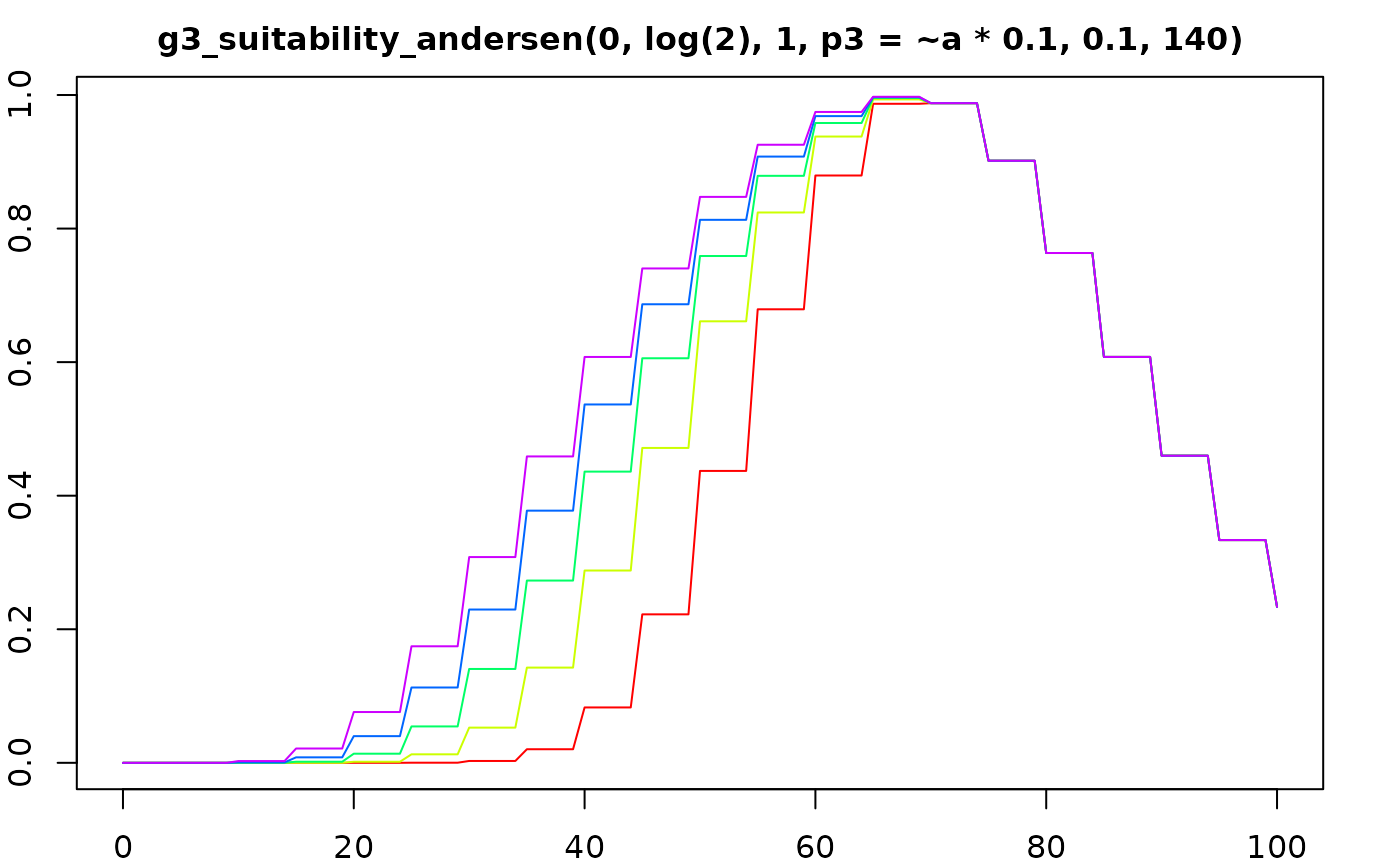suit_plot(g3_suitability_andersen(0, log(2), 1, 0.1, p4 = ~a * 0.1, 140))

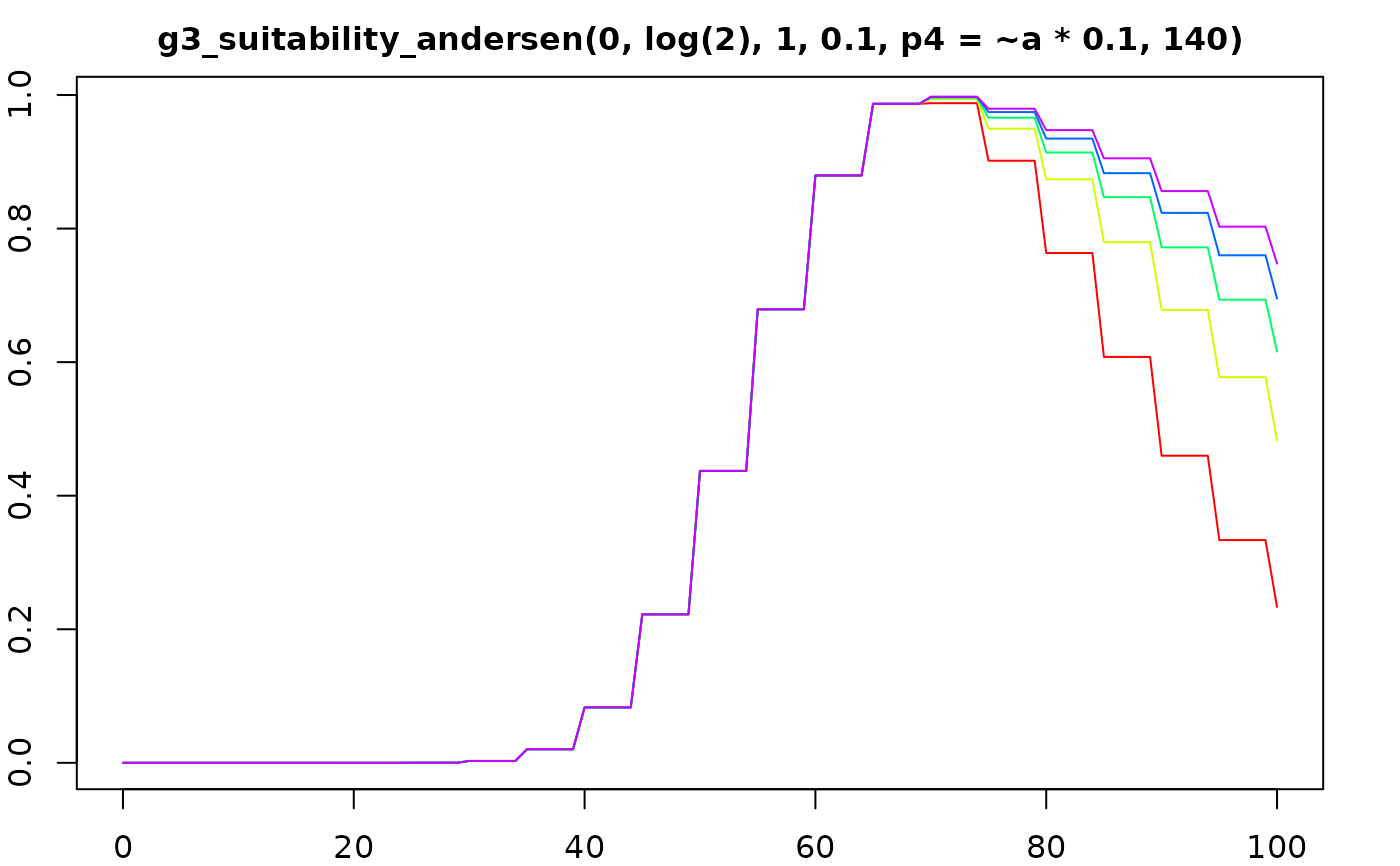suit_plot(g3_suitability_gamma(alpha = ~2 + a * 0.1, beta = 1, gamma = 40))

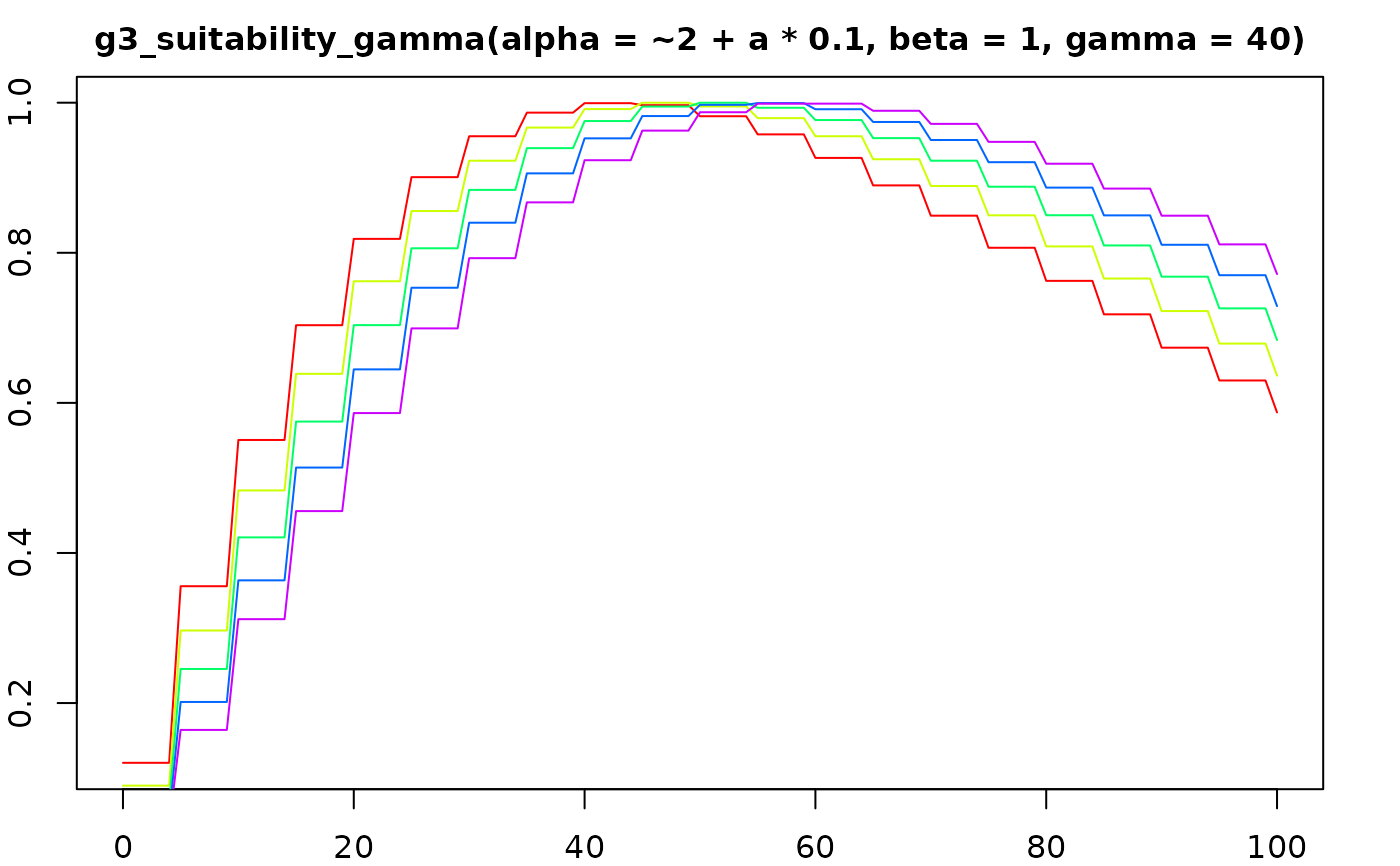suit_plot(g3_suitability_exponential(0, ~0.01 * a, 0, 1))

suit_plot(g3_suitability_straightline(alpha = 0.1, beta = ~0.01 * a))

suit_plot(g3_suitability_constant(~a * 0.1))

suit_plot(g3_suitability_richards(0, 0.05, 0, 1, ~0.1 * a))